An Illustrated Description of the Core Algorithm

This page contains an explanation of the algorithm behind the Python dendrogram code. This is demonstrated with a step by step example of how the algorithm constructs the tree structure of a very simple one-dimensional dataset. Even though this dataset is very simple, what is described applies to datasets with any number of dimensions.

Basic example

The following diagram shows a one-dimensional dataset (with flux versus position) in the solid black line, with the corresponding dendrogram for that dataset overplotted in green:

In the rest of this document, we will refer to the individual points in this dataset as pixels.

The way the algorithm works is to construct the tree starting from the brightest pixels in the dataset, and progressively adding fainter and fainter pixels. We will illustrate this by showing the current value being considered, with the following blue dashed line:

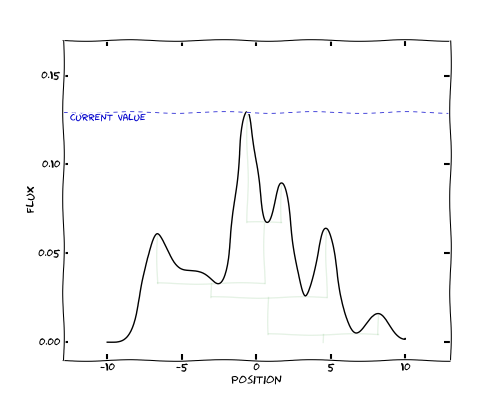
Let’s now start moving this line down, starting from the peak pixel in the dataset. We create our first structure from this pixel. We then move to the pixel with the next largest value, and each time, we decide whether to join the pixel to an existing structure, or create a new structure. We only start a new structure if the value of the pixel is greater than its immediate neighbors, and therefore is a local maximum. The first structure being constructed is shown below:

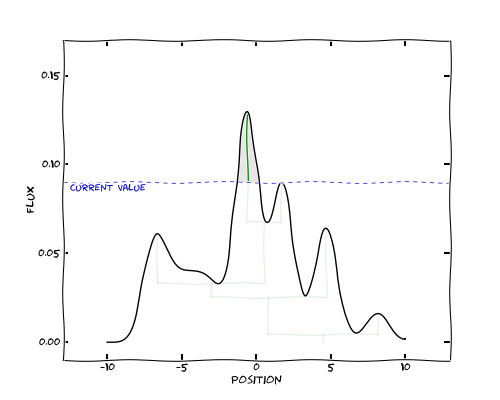
We have now found a local maximum, so rather than add this pixel to the first structure, we create a new structure. As we move further down, both structures keep growing, until we reach a pixel that is not a local maximum, and is adjacent to both existing structures:

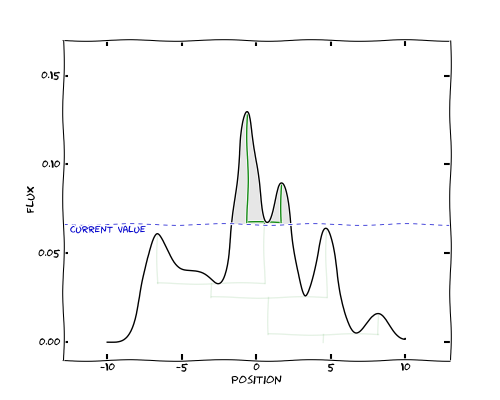
At this point, we merge the structures into a branch, which is shown by a green horizontal line. As we move down further, the branch continues to grow, and we very quickly find two more local maxima which cause new structures to be created:

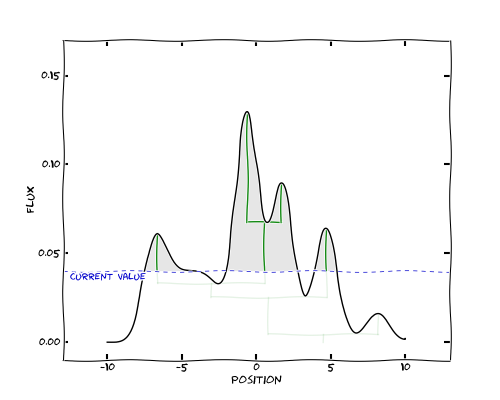
These structures eventually merge, and we end up with a single tree:

Accounting for noise

Setting a minimum value (min_value)

Most real-life datasets are likely to contain some level of noise, and below a certain value of the noise, there is no point in expanding the tree since it will not be measuring anything physical; new branches will be ‘noise spikes’. By default, the minimum value is set to negative infinity, which means all pixels are added to the tree. However, you will very likely want to change this so that only significant features above the noise are included.

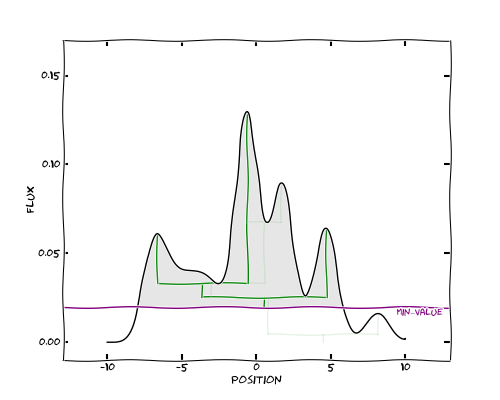
Let’s go back to the original data. We have left the outline of the complete tree for reference. We now set a minimum value, which we show below with the purple line. This is controlled by the min_value option in compute().

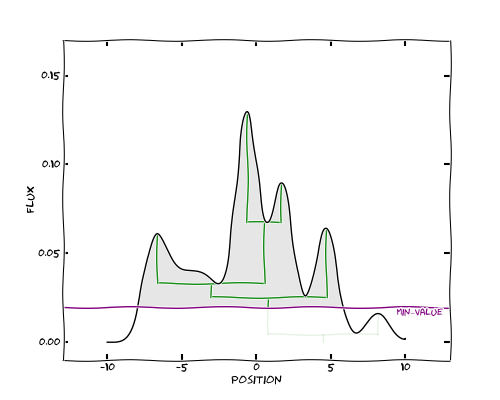
The effect on the tree is simply to get rid of (or prune) any structure peaking below this minimum. In this case, the peak on the right is no longer part of the tree since it is below the minimum specified value.

Setting a minimum significance for structures (min_delta)

If our data are noisy, we also want to avoid including local maxima that - while above the minimum absolute value specified above - are only identified because of noise, so we can also define a minimum height required for a structure to be retained. This is the min_delta parameter in compute(). We show the value corresponding to the current value being considered plus this minimum height:

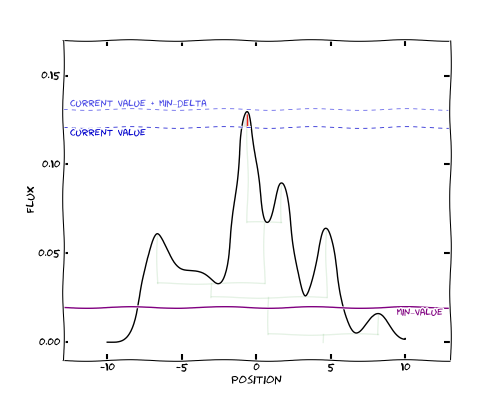
In this case, min_delta is set to 0.01. As we now move down in flux as before, the structure first appears red. This indicates that the structure is not yet part of the tree:

Once the height of the structure exceeds the minimum specified, the structure can now be considered part of the tree:

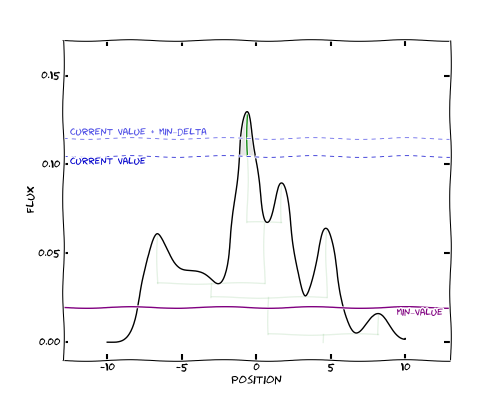
In this case, all structures that are above the minimum value are also all large enough to be significant, so the tree is the same as before:

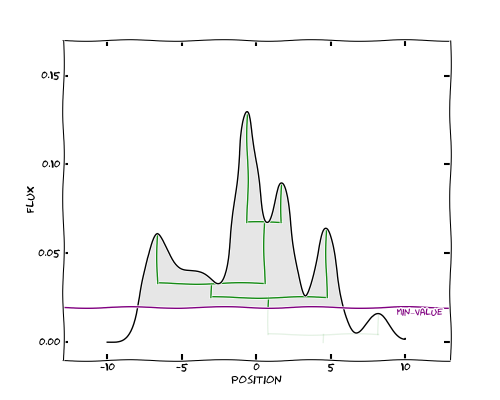
We can now repeat this experiment, but this time, with a larger minimum height for structures to be retained (min_delta=0.025). Once we reach the point where the second peak would have been merged, we can see that it is not high enough above the merging point to be considered an independent structure:

and the pixels are then simply added to the first structure, rather than creating a branch:

We can now see that the final tree looks a little different to the original one, because the second largest peak was deemed insignificant:

Additional options

In addition to the minimum height of a structure, it is also possible to specify the minimum number of pixels that a structure should contain in order to remain an independent structure (min_npix), and in the future, it will be possible to specify arbitrary criteria, such as the proximity to a given point or set of coordinates.